生き物の進化から学び、科学技術の発展を加速する。

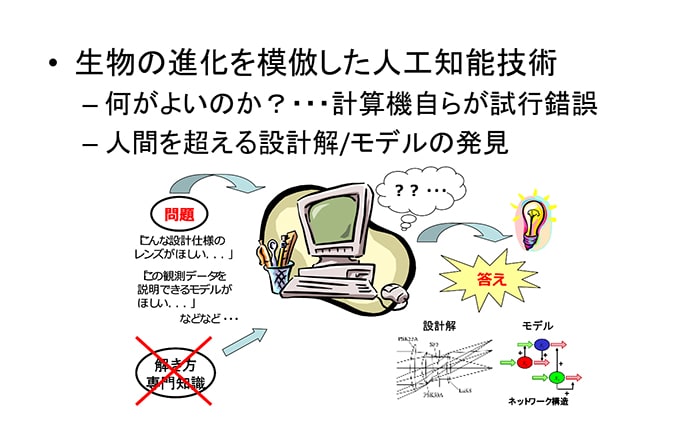
小野 ── 進化計算とは、生物の進化過程を模倣して、試行錯誤によって最適解を見つけるアルゴリズムです。何らかの問題を解く際、解を求めるための解法マニュアルがあれば、それに従って解くのが一番効率的でしょう。しかし、問題によっては先人が残した事例や手本が全くないものもあります。そうなると、試行錯誤してみるしかありません。環境の変化に対応して生存競争を生き抜いた生物の進化過程は、まさに「手本のない問題解決」の典型です。そこから学び、前例のない問題に取り組む手法として体系化しているのが進化計算の研究です。

小野 ── 身近な問題ではすでに進化計算が使われています。たとえば、N700系新幹線の先頭車両のノーズ形状の設計には進化計算が使われました^[1]。新幹線のノーズ形状は、トンネルに突入する際に発生する騒音の軽減を求めて進化してきました。N700系以前には、設計者の経験を基に、世代が代わるたびにノーズを尖らせていきました。ところが、ノーズが尖り過ぎて、さらなる騒音低減を望むなら先頭車両に乗せる乗客を減らしたうえ、ホームに収まらないほど長くするしかないという状況になってしまったのです。一度「経験に基づく設計」から離れ、「事例や手本によらない設計」を考える必要が出てきました。

そこで進化計算の一種である遺伝的アルゴリズムを適用した結果、これまでとは異質な形状が設計解として見つかり、これまで以上の速度で運転しても大きな騒音が発生しないように設計できました。同様の手法は、国産旅客機MRJの翼の形状^[2]やタイヤの形状^[3]など、飛躍的な性能向上を求める機械設計の分野で使われています。

小野 ── エキスパートシステムと呼ばれた一定のルールに沿って問題を解くかつてのAIは、解法マニュアルそのものでした。だから知識の蓄積がないと問題が解けません。そして、現在広く活用されるようになった深層学習（ディープラーニング）をはじめとする機械学習系のAIは、解法マニュアルは不要ですが、過去の事例から得られたデータがないと解を探り出せません。いずれにしてもAIでは、解を求めるためにマニュアルかデータが必要になります。

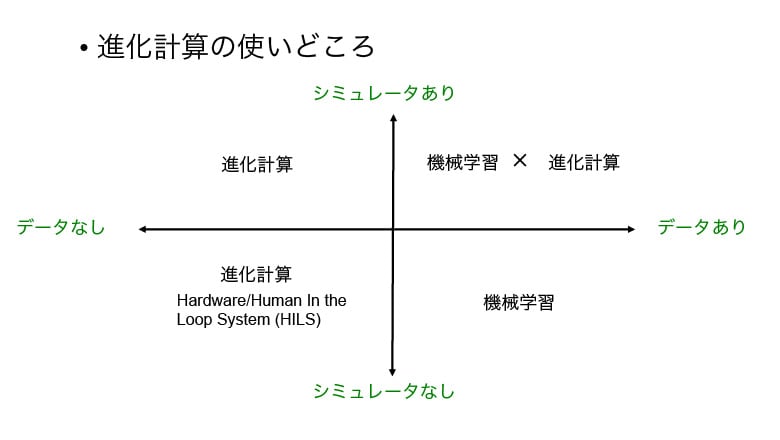
一方の進化計算は、未知の環境に放り出されて、一定の仕事の成果を出さなければならないような状況に向いている手法です。必要なのはシミュレータなどのブラックボックスな環境と、そこで達成すべき目的です。進化計算はこうした状況下で失敗覚悟の試行錯誤を繰り返し、得られた結果が目的に沿っているのかを評価しながらより良い解を探求していきます。

機械学習の分野では、環境からの報酬を手がかりに行動戦略を学ぶ「強化学習」と呼ぶ手法があります。試行錯誤による結果を評価し、より良い解を求める点で進化計算と考え方は同じです。ただし、強化学習ではロボットやエージェントなどの行動学習に特化した定式化になっているため、これらの問題では進化計算よりも効率よく学習を進めることができます。一方、進化計算は、強化学習が対象としているタスクにも適用可能であり、より汎用性の高い問題解決手法になっています。

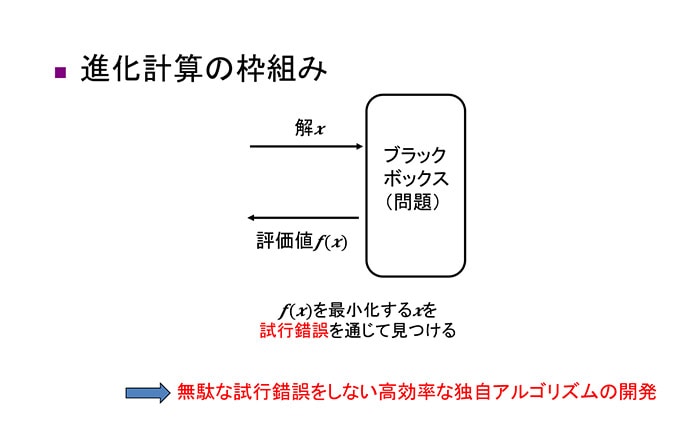
小野 ── まず、評価値を求めるためのブラックボックスな環境を用意します。たとえば、新幹線のノーズ設計では、ノーズ周りにおける空気の流れなどを再現するシミュレータを用意します。そして、そこに勝手に設定した何種類かの解の候補を入れて環境で起きた現象を評価し、それが目的に合った良い解なのか悪い解なのかを評価します。そして、最も高い評価値を得た解を設計解とするのです。

ただし、このままでは単に試行錯誤しただけで終わってしまいます。むやみに解の候補をブラックボックスに入力したのでは、良い解を得るまでに時間がかかってしまいます。旅客機の翼の形状のような複雑な現象が関わるケースにおける解の評価は、シミュレータでひとつの解を評価するだけで一日がかりです。そのため、無駄な試行錯誤をすることなくより良い解を求める方法が求められます。ここが私たちの腕の見せ所です。

小野 ── もっとも古典的な進化計算の手法として、「ビットストリング遺伝的アルゴリズム（ビットストリングGA）」と呼ばれるものがあります。1970年代にジョン・H・ホランド氏が開発した、試行錯誤を効率化する手法です^[4]。この手法では、解の候補を0と1のビットストリングで表現し、ランダムに設定した複数の解の候補を検証したあと、結果が良かった解同士の特徴を組み合わせて「次世代の解の候補」をつくります。こうした作業を何世代にもわたって繰り返すことで、複数の解の候補はだんだんと最適解の近くへとにじり寄っていきます。「良い結果が得られた解の候補には、良い結果をもたらす何らかの要因が含まれているに違いない」という仮定に基づいて、より目的に合った解を探求していきます。次世代の解を生み出す方法としては、二つの解の候補のビットストリングの間で、各ビットを50%の確率で交換することにより新しい解の候補を生成するという方法があります。この方法は、一様交叉と呼ばれますが、それほど効率よく優れた解を探り出せません。

小野 ── その通りです。例として、最近、小野研究室で開発したDX-NES （Distance-based Exponential Natural Evolution Strategy）^[5]と呼ばれるアルゴリズムをご紹介しましょう。DX-NESは、2008年にWirestraらが考案した自然進化戦略（Natural Evolution Strategy, NES）^[6]を発展させた方法であり、ビットストリングGAよりもかなり少ない数の解の候補を生成するだけで効率よく最適解に近づくことができます。

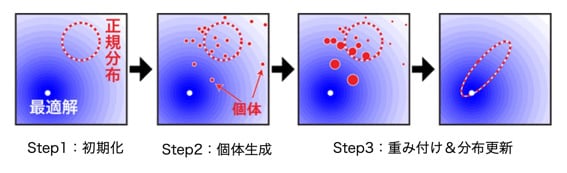
DX-NESでは、まず任意の解を決めてその解を中心にした正規分布を考えます。変数が2つある2次元の問題では、平面内の1点を頂点にする山のようなすそ野を持った楕円形の確率分布を持つ領域になります。そして、正規分布に従って生成される解の候補の評価値の期待値を改善するように、正規分布の重心と形を学習します。具体的には、正規分布に従って第1世代の解の候補をいくつかつくり出します。続いてそれぞれの解の候補の評価値を求め、その評価値を基に重み付けし、次世代の解の候補を作るための正規分布の重心と形を定めます。こうすると、高い評価値が得られた解がある方向へと正規分布の重心がズルズルと動き、最適解がある方向により多くの解を生成できるようになるのです。

さらに、正規分布の重心が動いているときは、重心から遠い良い解の候補に大きな重みを与えて学習率を大きな値にし、それ以外のときは良い解の候補に大きな重みを与えて学習率を小さな値に設定するという工夫を導入しています。これにより、最適解から遠いときには、世代間での正規分布の重心が大きく動き、近づくと動きが小さくなり、さらに効率よく解を探り出せます。

DX-NESの解を探り出す効率は、簡単なベンチマーク問題である20次元Sphere関数で最適解を覆うように初期化領域を設定した場合、さきほど紹介したビットストリングGAの100倍以上に向上します。それまで、1,000万円もするPCクラスタでないと解けなかった問題が、1台の安価なPCで解けるようになってしまうのです。最適解を覆わないように初期化領域を設定した場合や、変数間に依存関係がある関数などの難しい問題になると、DX-NESは最適解を見つけられますが、ビットストリングGAは最適解を見つけられなくなってしまいます。アイデア次第でこうした劇的効果が得られる場合もある点が、この研究の醍醐味ですね。

小野 ── そうですね。これまでの情報処理の手法では、決して解けなかったような問題も工夫次第で解けるようになるのでやりがいのある研究だと思います。

たとえば、困難な問題として有名な「巡回セールスマン問題^*1」と呼ばれる組合せ最適化問題も解くことができます。巡回セールスマン問題は、訪問先として複数の都市が与えられたとき、すべての都市を一筆書きで訪問する最短の巡回経路（最適解）を見つける問題です。巡回経路の候補の数は有限なので、原理的にはすべての巡回経路を洗い出せば必ず最適解を見つけられるはずです。しかし、都市数がたった30都市の問題でも、スーパーコンピュータを使ったとしても、生きている間には最適解が得られる保証がないほど長時間の計算が必要になります。

小野 ── そんな問題も進化計算を活用すれば、最適解を見つける保証はありませんが、かなり効率よく良い解を見つけることができます。たとえば、図5に示すような、10万から20万点のドットで点描された「モナ・リザ」や「ゴッホ」などの名画を対象に、すべての点をつないで一筆書きした場合の最短経路を求める6つのベンチマーク問題があります^[7]。つまり訪問先が10万から20万都市ある巡回セールスマン問題というわけです。これらのベンチマーク問題では、訪問先が30都市の巡回セールスマン問題をはるかに上回る膨大な計算が必要になります。

この問題に対して、2013年に私たちの研究室で開発した進化計算アルゴリズムを、東工大のスーパーコンピュータTSUBAME2.0の30台の計算ノード上で並列に実行したところ、約5時間（10万都市問題）～約30時間（20万都市問題）で、これまでに知られている最良解（既知最良解）に対する誤差が約0.0063%（10万都市問題）～約0.0075%（20万都市問題）の解を得ることができました。

小野 ── さらに、乱数系列を変えた同じアルゴリズムで、改めて6問それぞれの最短経路を求めるチャレンジを10回ずつ行い、得られた解の上位10%の解を合わせて次世代の解の候補とし、これを用いてさらに進化計算アルゴリズムで最短経路を求めました。その結果、10万都市、14万都市、16万都市、20万都市の4つの問題で既知最良解（発見された経路長はそれぞれ5,757,191、6,810,665、7,619,953、8,171,677）を発見し、12万都市と18万都市の2つの問題で既知最良解よりも良い解（発見された経路長はそれぞれ6,543,609、7,888,731）を発見することに成功しました^[8]。

小野 ── 量子アニーリング・マシンは、非常に魅力的なハードウェアだと思います。量子アニーリング・マシンの専門家ではないのではっきりしたことは言えませんが、多分、ハードウェアが順調に進化すれば、こうした問題は量子アニーリングのほうが効率よく解けるようになる可能性が高いと思います。ただし、量子アニーリングを上手に活用するには、進化計算の研究で得られた知見が有効に活用できると期待されます。シミュレーテッド・アニーリングや進化計算、タブー探索などは、最適化問題の解法の中でも類似の原理を基にしており、「メタヒューリスティックス」とよばれる最適化手法として一括りにされています。同種の手法ですから、実問題を量子アニーリング・マシンで解く問題に落とす際には同じ知見が役立つと考えています。

小野 ── はい。いま、量子アニーリングのソフトウェア技術者が足りない、もしくは将来的に足りなくなると言われています。進化計算の研究を通して蓄積された知見は、将来の量子コンピュータ活用に役立つと期待しています。

小野 ── 学生時代から人の知的な活動、とくに設計手法などに興味がありました。効果的な設計や作業はどのように行われているのか、困難な問題とはそもそも何が難しいのか、知りたかったのです。学部3年生の時に人工知能関係の授業を受け、そこで遺伝的アルゴリズムが紹介されました。そこで簡単な試行錯誤の繰り返しで困難な問題が解けることを知り、その不思議な面白さに魅了されて、そこから今まで約25年間研究を続けています。

小野 ── より速く困難な問題を解ける方向へと進化しています。自然界では、驚くような進化が起きます。しかし、進化のスピードは極めて遅く、決して効率のよいものではありません。それを効率化することで現在の生物が到達できていないような能力を見つけ出すことができます。たとえば、鳥にインスパイアされて飛行機ができました。鳥が音速を超えて飛ぶことはできませんが、人がつくったジェット機なら可能です。進化計算は、超音速の領域で飛行機をさらに進化させるための解も探ることができます。

また現在では、変数が1万もあるような大規模なブラックボックス関数最適化問題も解けるようになってきています。多くの工学的問題では、変数は高々100程度です。しかし、ある複雑な現象を説明するためのモデルを構築するというモデリングの問題になると、さらに多くの変数を扱う必要が出てきます。たとえば、遺伝子間の相互作用のパラメータを決める医学・生物学の問題を扱う際には、前述した「変数が1万もあるような」大規模な問題が出てきます。進化計算では、こうした医学・生物学の問題の問題解決にも役立ちます。また、経済学的な現象をモデル化し、データにフィッティングさせるといった問題の解決にも役立ちます。モデリングの問題では、変数の数は1万にとどまらず、10万、100万の問題も存在しますので、さらなるアルゴリズムの性能向上が望まれています。

小野 ── 本当にそう感じます。ただし、そう簡単ではありません。研究では、ベンチマーク用の問題を使ってより高速に解ける方法を考案するのですが、ベンチマークで良い結果が得られても、現実の類似問題に適用したら思わしい効果が得られなかった――という場合が多いのです。

小野 ── 「ベンチマークの問題を解く」という目的だけのために最適化されたアルゴリズムになってしまうからです。現実の問題からベンチマークをつくる際に落としてしまった性質があるわけです。実際に役立つアルゴリズムにするためには、それを取り入れて困難な問題、複雑なプロセスに対応できるアルゴリズムへと進化させる必要があります。

小野 ── そうなのです。実は、そのことは「ノーフリーランチ定理」^[9]として知られています。ありとあらゆる問題に対応できる完全に汎用なアルゴリズムをつくろうとすると、結局は「もっとも非効率なランダムサーチと平均的な性能の観点で一緒になってしまう」というものです。そのため、現実の問題を解く効率を高めるには、工学や科学の分野において解くべき実問題に広く現れる性質を見つけ出して、これをうまく利用したアルゴリズムを作る必要があります。私たちは共通の性質を持った問題群を「問題クラス」と呼んでいますが、これをなるべく一般化しながら効率的に解ける問題の範囲を広げています。そのため、つくっては試しを繰り返しながら手法を進化させていく必要があります。

小野 ── さらに大規模な問題、解決困難な問題に取り組んでいきたいと思っています。互いに相反する多くの目的を同時に満たす解を求めるという「多目的最適化問題」と呼ばれる問題があります。多目的最適化問題は、目指す目的の数が増えると扱う変数も増え、問題自体がどんどん複雑になるのが特徴です。ところが、こうした問題は現実の製品開発などではよく見られる問題なのです。

複数車種の同時最適化のベンチマーク問題 ^[10]を例に挙げましょう。自動車業界では、クルマの製造コストを減らすため、小型車、SUV、大型車といった複数の車種の間で、なるべく同じ部品を使いたいという発想があります。部材を大量発注できるので、コストダウンできるからです。しかし、大型車の部材だけで小型車をつくると当然重量が増えますから、燃費が悪くなります。では、小型車に合わせればよいかというと、衝突安全性能の確保の観点から大型車には相応の部品を使う必要があるのです。つまり、共通部品点数と重量は、トレードオフの関係にあります。

こうしたトレードオフの関係が存在する問題には、最適解が複数存在します。これを「パレート解」と呼びます。共通部品の共通化を重視した最適解もあれば、重量の軽減を重視した最適解もあるのです。

小野 ── こうした問題を迅速に解くことができれば、世の中に大きなインパクトを与えられます。それを求める人も多く、これらの問題を題材にして、多くの大学が解法を競うコンペティションが開催されています。

じつは、さきほどお話した「複数車種の同時最適化のベンチマーク問題」もコンペティションのために提供された問題です^[11]。また、月探査の着陸船の最適な着陸地点を見つけ出す問題の解法を競うコンペティションも開催されました^[12]。日陰になる日数を最小化し、地球との通信時間を最大化して、なるべく平らな着陸地点を選ぶというものです。

最近では、機械学習やロボットの制御でも同様ですが、研究を進めるうえでこうしたコンペティションへの取り組みがとても重要になっています。高等専門学校が積極的に取り組むロボコンも、高専生の技術力や学習意欲を高めるのに非常に役立っていると思います。明確な目標の実現に向けて多くの試行錯誤と失敗を経験することは、研究を推し進めるうえで非常に重要なのです。

小野 ── ディスカッションを重視し、常に「なぜ」を問いかけて、本人に考えてもらうように心がけています。中途半端な状態で納得せず、上手くいっても、いかなくても、なぜそうした結果が得られたのかひたすら問いかけるよう指導しています。

小野 ── とても重要です。取り組む問題が何なのかを言葉にできたら、研究としては相当いい線を行っていると思います。ゼミでは「1時間説明してもらって、その後1時間以上かけて研究室メンバー全員で質疑応答とディスカッションを行う」という時間をかけたスタイルで進めています。

ディスカッションの際は、まず、説明に用いる言葉の定義を明確にしてから議論を進めます。私たちの研究で扱う対象は抽象的なものが多いので、ディスカッションで用いる言葉を明確に定義しないと話が全く噛み合わなくなってしまうからです。そして、しっかりと問いかけができてはじめて、自分が持っていない視点を持つ人から貴重な気づきを得ることができます。研究の過程で得た結果に、時にもやもやとした違和感を覚えることがあります。しかし、そのことを誰にも語らないまま、意識の下に沈めてしまいがちです。それをまず言葉にして顕在化させないと、新しい知見は得られません。

小野 ── 学生が社会に出た際、当然、研究室で得た専門知識も活かして欲しいのですが、それ以上に研究の過程で培った問題を言葉にできるスキルや、相手と情報交換して取り組むべき課題を見つけるスキルを活かしてもらえたらうれしいです。そして、人を幸せにする、ワクワクするような技術を開発してほしいと考えています。